 inTrustPlus
inTrustPlus
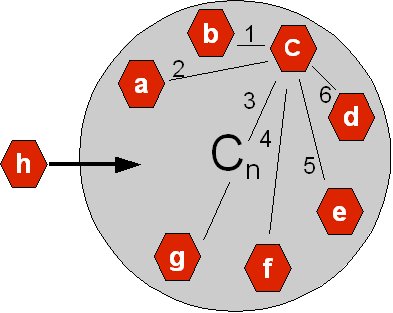
In the above illustration the gray circle symbolizes a network and the red hexagons the nodes (population) of the network. The 6 arcs extending from the C hexagon symbolize C's connections to the other members of the network. There are 7 members. C can make 6 connections amongst the network's population - and so can all the others, though we have refrained from drawing their arcs as well.
Though in most situations the value of these connections would vary – for the sake of this example we will say that they all have an equal value of 1, and thus, the network benefit for C is 6, just as it is for each of the other nodes in the population. The sum value for the entire network is 42 (7x6).
If node h enters the network, the benefit for each of the existing members will be increased by by one, and the sum benefit for them all would now be 49, but we must also factor in the benefit for the new member h, which is also 7, making the sum benefit for all members = 56.
Now according to Metcalfe's law the increase in benefit, when expanding from 7 members to 8 - that is from a benefit sum of 42 to a benefit sum of 56, should be proportional to the increase in the square of the number of members, that is from 72 = 49 to 82 = 64.
Since 49/64 and 42/56 are equal, so far Metcalfe would seem to be right.
But how did we arrive at the benefit value for each member? Apparently, in a completely arbitrary fashion. We made two naïve assumptions: one) that a connection was always a benefit, and two) that all connection benefits were of equal value.
In real life, in any of the myriad networks we participate in, we would hardly value each node, or connection, as being of equal value and, for that matter, often consider some of our connections without value whatsoever -a nuisance.
The point is that Metcalfe is not describing the benefits of actual usage, but rather the benefits of potential use. Metcalfe is describing a communication network. A communication network is a system of potential, rather than actual - use.
In order to apply Metcalfe's law to real life situations, we would want to know how potential utility relates to realizable utility. And we would want to know something about the costs involved: The costs of maintaining potentials and the cost of utilizing them.
©Greg FitzPatrick 
We work in order to gain something. Rational behaviour dictates that we will attempt to gain as much as possible while exerting as little effort as possible. In all endeavor there appears to be a dynamic relationship between effort and gain. That is - the ratio between the time and energy we spend and the benefits derived is never a constant.
You can only polish a window so much before your work will seem superfluous. The glass will probably look just fine after a few wipes, even though it won't be perfect. You can keep scrubbing away after those last little flecks of dirt for quite some time, but the returns of your work (to the average observer at least) will be increasingly insignificant the longer you continue, and the time and effort you put in will be time and effort you could perhaps be spending better somewhere else - on other windows for example.
Note: Since I cover the subjects of bounded rationality and emotional gratification in other chapters, I wont go into them here - but, yes, it is possible that the rewards for our window washer are not so simply measured as in the opinion of "the average observer".
Another naive example is mining: We discover some gold and we start to dig. Our effort is digging - our reward is gold. As our excavation progresses we will hope to find a pattern in the amount of gold harvested relative to our effort. We are looking for a vein, a core. We are aware that gold is not distributed equally about the surface of the earth.
We might have been lucky and found the vein straight off, or we might need to explore a bit more, digging here and there in some orderly fashion that will increase our chances of finding the concentration we are looking for. Once the core is found we will continue digging outwards from it. Eventually we will reach a point where it is futile to dig further.
The point is, having knowledge about the distribution of gold deposits, digging for gold just anywhere is not rational behavior while digging where one knows there is a concentration of profitably harvestable gold is. As the amount of gold found becomes increasingly sparse in proportion to the amount of digging required we will begin to doubt the rationality of carrying on in the same direction.
We realize that somewhere in between lots-of-gold and no-gold-at-all there is a breaking point where the cost of effort has surpassed the returns on effort. Unfortunately mineral deposits like wins in a poker game, and many other potential gains, do not present themselves in a linear fashion. We are often driven far past the break-even point in the hope of getting lucky - finding a new vein. And sometimes we do.
Though technology does not eliminate the dynamic relationship twixt effort and gain, it does move the breaking point so that the benefit curve remains above the effort curve further out from the profitable core. And this gives rise to the argument that many natural resources are not as limited as we reckon them to be since technology will make costly exploration and extraction methods cheaper (move the breaking point between cost and benefit outwards).
Soft IT, due to its commonalized-commoditized nature, pushes the cost-benefit breaking point to extremities unparalleled in the physical world, and tends to straighten out the non-linear or erratic nature of exploration.
©Greg FitzPatrick 
-
In fielding the objection that electronic games are available as both proprietary single-purpose boxes connected to televisions (aka video games), and as software for the general-purpose computer (aka computer games) I neglected to point out that my examples scribbled on the whiteboard were primarily production devices: Number crunchers, word processors, layout tools, sound processors, image processors, CAD and CAM, and video processors. These were products packaged for commercial-professional use.
-
With the exception of number crunchers which were introduced in an era that had yet to experience the general-purpose computer, these apparatus were almost always entered into the market at price points above that of the general-purpose computer, sometime by multiples of 2 or 3.
-
There are a plethora of digital devices (digiphernalia) that are not about to be subsumed by the general-purpose computer, eg. clocks, radios, TVs, game-boys, PDAs, telephones, and so on. Though these items might be task-specifically outperformed by the general-purpose computer, they are far superior in utility-specificity (size, portability, aesthetics, etc.) and their price points are invariably less, in some cases fractionally so, than the general purpose computer. (You can buy a digital watch for a dollar)
-
Since most of these devices now use the equivalent of a computer's CPU, (as do microwave ovens, toasters, vacuum cleaners etc.) they do avail themselves of many of the advantageous developments made in general-purpose computing. And sometimes they take the lead in innovation. This area is known in the industry as embedded systems.
-
Most media broadcasting is still analogue – though a more efficient use of air waves leads governments to mandate a shift towards digital broadcasting for both radio and television.
-
One aspect of the discussion which you should be aware of is the fact that there are two incomparable paradigms of video imaging – that of the television (interlaced) and that of the computer screen (progressive). And though you may see TV on your computer and experience the Internet on your TV – this is only accomplished by the addition of extra layers of interface and processing power with sub-optimal results.
-
The IT industry has lobbied presently for government mandated migration from interlaced to progressive video under the banner of “convergence”, but it has been mostly an uphill battle. HD- television has been seen as logical point of convergence between the two systems, but HD-television has become a very messy affair.
- If there were not two widespread imaging platforms in our homes due to historical developments, we would not have these two particular paradigms of gaming (TV & Computer), but other specificities such as portability, which will give rise to alternative solutions.
©Greg FitzPatrick 
