Metcalfe's Law

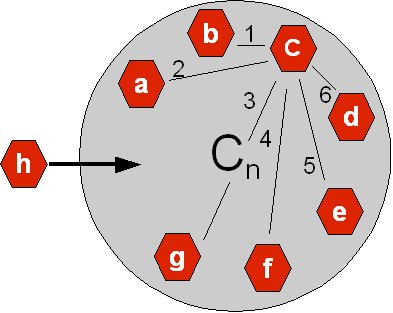
In the above illustration the gray circle symbolizes a network and the red hexagons the nodes (population) of the network. The 6 arcs extending from the C hexagon symbolize C's connections to the other members of the network. There are 7 members. C can make 6 connections amongst the network's population - and so can all the others, though we have refrained from drawing their arcs as well.
Though in most situations the value of these connections would vary – for the sake of this example we will say that they all have an equal value of 1, and thus, the network benefit for C is 6, just as it is for each of the other nodes in the population. The sum value for the entire network is 42 (7x6).
If node h enters the network, the benefit for each of the existing members will be increased by by one, and the sum benefit for them all would now be 49, but we must also factor in the benefit for the new member h, which is also 7, making the sum benefit for all members = 56.
Now according to Metcalfe's law the increase in benefit, when expanding from 7 members to 8 - that is from a benefit sum of 42 to a benefit sum of 56, should be proportional to the increase in the square of the number of members, that is from 7² = 49 to 8² = 64.
Since 49/64 and 42/56 are equal, so far Metcalfe would seem to be right.
But how did we arrive at the benefit value for each member? Apparently, in a completely arbitrary fashion. We made two naïve assumptions: one) that a connection was always a benefit, and two) that all connection benefits were of equal value.

In real life, in any of the myriad networks we participate in, we would hardly value each node, or connection, as being of equal value and, for that matter, often consider some of our connections without value whatsoever -a nuisance.

The point is that Metcalfe is not describing the benefits of actual usage, but rather the benefits of potential use. Metcalfe is describing a communication network. A communication network is a system of potential, rather than actual - use.

In order to apply Metcalfe's law to real life situations, we would want to know how potential utility relates to realizable utility. And we would want to know something about the costs involved: The costs of maintaining potentials and the cost of utilizing them.

- posted by Greg FitzPatrick click for separate chapter layout